TensorFlow强化学习入门（1.5）——上下文赌博机

Arthur JulianiSimple Reinforcement Learning with Tensorflow Part 1.5: Contextual Bandits

注意：本文为该系类文章中（1）和（2）之间的过渡

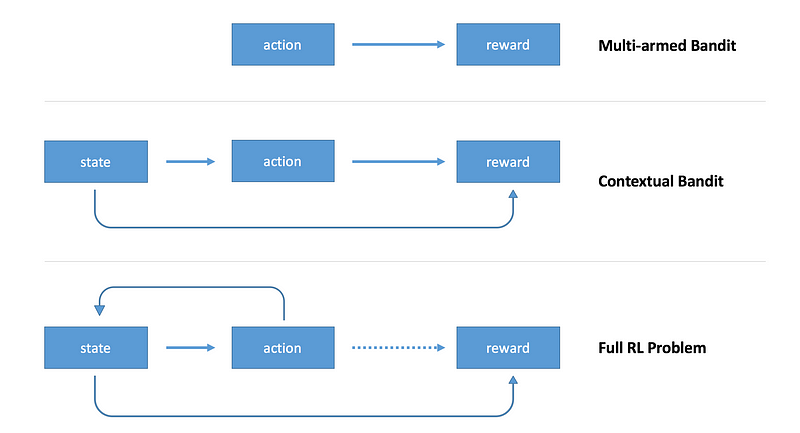
在上一篇文章中我们简要介绍了强化学习并构建了一个简单的agent来解决多臂赌博机问题。在多臂赌博机问题中agent不需要考虑所处环境的状态，只要通过学习确定那一个行动是最优的即可。在不考虑环境状态时，任一时间点上的最优决策是所有时刻最优的决策。在本文结束后，我们会建立一个完备的强化学习问题：问题中存在环境状态并且下一时刻的状态取决于上一步的行动，决策的收益也是延迟发放的。

从无状态的场景迁移到完备的强化学习需要解决很多问题，下面我将提供一个实例并展示如何解决它。希望新接触到强化学习的同学可以从这个过程中有所收获。本文中我将着重讲解什么是状态，但本文中的状态不是由之前的状态和行动决定的。延迟收益的问题本文也不做讨论，这两个问题都将留到下篇文章解决。本文这种强化学习问题的简化版本又被称为上下文赌博机问题。

上下文赌博机

在上文讨论的多臂赌博机问题中，我们只有一个赌博机，可以理解为一台老虎机。agent的决策范围只是选择多个的赌博机臂中的一个，不同的决策对应获得+1或-1收益概率的不同。当我们的agent总是选择获得正收益概率最大的机臂时，我们认为这个问题得到了解决。因为所有的决策和结果都不会影响环境状态，所以我们在设计agent的时候忽略了环境状态。

上下文赌博机引入了 状态 的概念。agent可以利用状态中对环境的表述作出更加明智的决策。在引入这个概念之后，我们把之前的单个赌博机扩展为多个赌博机。环境状态可以告诉我们我们当前使用的是什么样的赌博机，这个agent的目标从对单个赌博机作出最优决策变为对任意数量的赌博机作出最优决策。因为不同赌博机的赌博机臂会有不同的赔率，所以我们的agent需要基于环境状态作出决策，否则它不能在所有的情况下都获得最大的收益。为了解决这一问题，我们将用TensorFlow构架一个单层神经网络来接受状态变量并作出相应行动。通过策略梯度的更新方法，我们可以使网络学会作出收益最大的行动。下面给出示例代码：

import tensorflow as tf
import tensorflow.contrib.slim as slim
import numpy as np


# 定义我们的上下文赌博机
# 在本例中，我们创建三个四臂赌博机，即每个赌博机有四个机臂供选择，每个赌博机的机臂有着不同的赔率。
# pullBandit函数用于生成均值为0的正态分布的随机数。bandit的值越小，得到正收益的概率越大。
# 我们的目标：agent可以根据给定的赌博机选择收益率最大的赌博机臂
class contextual_bandit():
    def __init__(self):
        self.state = 0
        # 设定我们的赌博机，收益率最大的赌博机臂编号分别为4，2，1
        self.bandits = np.array([[0.2, 0, -0.0, -5], [0.1, -5, 1, 0.25], [-5, 5, 5, 5]])
        self.num_bandits = self.bandits.shape[0]
        self.num_actions = self.bandits.shape[1]
    
    def getBandit(self):
        self.state = np.random.randint(0, len(self.bandits))
        # 每个episode返回一个随机的状态
        return self.state
    
    def pullArm(self, action):
        # 生成随机数
        bandit = self.bandits[self.state, action]
        result = np.random.randn(1)
        if result > bandit:
            # 返回正收益
            return 1
        else:
            # 返回负收益
            return -1


# 基于策略的Agent
# 下面创建我们的agent的神经网络，state（状态）为网络输入，这使得agent可以根据环境状态行动，这一提升也是该网络适用与完备强化学习的关键改动。
# agent使用了一个简单的权重集，据此它可以为选定的赌博机返回价值预估，我们使用策略梯度方法来更新agent
class agent():
    def __init__(self, lr, s_size, a_size):
        # 前馈部分，网络接受状态值，作出决策
        self.state_in = tf.placeholder(shape=[1], dtype=tf.int32)
        state_in_OH = slim.one_hot_encoding(self.state_in, s_size)
        output = slim.fully_connected(state_in_OH, a_size, biases_initializer=None, activation_fn=tf.nn.sigmoid, weights_initializer=tf.ones_initializer())
        self.output = tf.reshape(output, [-1])
        self.chosen_action = tf.argmax(self.output, 0)
        
        # 训练流程，我们将得到的收益和行为送入网络来计算损失值并据此更新网络
        self.reward_holder = tf.placeholder(shape=[1], dtype=tf.float32)
        self.action_holder = tf.placeholder(shape=[1], dtype=tf.int32)
        self.responsible_weight = tf.slice(self.output, self.action_holder, [1])
        self.loss = -(tf.log(self.responsible_weight)*self.reward_holder)
        optimizer = tf.train.GradientDescentOptimizer(learning_rate=lr)
        self.update = optimizer.minimize(self.loss)

# 训练网络
tf.reset_default_graph() # 重置TensorFlow计算图

cBandit = contextual_bandit() # 加载赌博机
myAgent = agent(lr=0.001, s_size=cBandit.num_bandits, a_size=cBandit.num_actions) # 加载agent
weights = tf.trainable_variables()[0] # 权重

total_episodes = 10000 # 设置agent训练的episodes数
total_reward = np.zeros([cBandit.num_bandits, cBandit.num_actions]) # 初始化分数
e = 0.1 # 随机行动概率

init = tf.global_variables_initializer()

# 启动TensorFlow计算图
with tf.Session() as sess:
    sess.run(init)
    i = 0
    while i < total_episodes:
        s = cBandit.getBandit() # 获取环境状态
        # 决定是根据网络选择赌博机还是随机选择赌博机
        if np.random.rand(1) < e:
            action = np.random.randint(cBandit.num_actions)
        else:
            action = sess.run(myAgent.chosen_action, feed_dict={myAgent.state_in:[s]})
            reward = cBandit.pullArm(action) # 行动并返回收益
            # 更新网络
            feed_dict={myAgent.reward_holder:[reward], myAgent.action_holder:[action], myAgent.state_in:[s]}
            _, ww = sess.run([myAgent.update, weights], feed_dict=feed_dict)
            # 更新本次运行的得分
            total_reward[s, action] += reward
            if i % 500 == 0:
                print(str(cBandit.num_bandits) + "台赌博机的平均得分: " + str(np.mean(total_reward, axis=1)))
            i += 1
for a in range(cBandit.num_bandits):
    print("我们的agent认为" + str(np.argmax(ww[a])+1) + "号机臂对于" + str(a+1) + " 号赌博机是最优决策")
    if np.argmax(ww[a]) == np.argmin(cBandit.bandits[a]):
        print("...经检验正确！")
    else:
        print("...经检验错误！")

3台赌博机的平均得分: [-0.25  0.    0.  ]
3台赌博机的平均得分: [39.25 43.75 39.25]
3台赌博机的平均得分: [86.25 79.75 81.25]
3台赌博机的平均得分: [126.75 119.5  126.  ]
3台赌博机的平均得分: [164.25 159.5  173.5 ]
3台赌博机的平均得分: [208.25 204.75 209.25]
3台赌博机的平均得分: [249.5  244.25 253.5 ]
3台赌博机的平均得分: [290.5  285.   296.75]
3台赌博机的平均得分: [334.   323.   340.25]
3台赌博机的平均得分: [378.   368.25 376.  ]
3台赌博机的平均得分: [418.75 408.75 419.75]
3台赌博机的平均得分: [464.   450.75 457.5 ]
3台赌博机的平均得分: [506.75 493.   497.5 ]
3台赌博机的平均得分: [550.75 534.75 536.75]
3台赌博机的平均得分: [590.5  579.5  577.25]
3台赌博机的平均得分: [632.   620.25 620.  ]
3台赌博机的平均得分: [672.   659.75 665.5 ]
3台赌博机的平均得分: [714.   698.75 709.5 ]
3台赌博机的平均得分: [756.75 739.   751.5 ]
3台赌博机的平均得分: [798.   779.   795.25]
我们的agent认为4号机臂对于1 号赌博机是最优决策
...经检验正确！
我们的agent认为2号机臂对于2 号赌博机是最优决策
...经检验正确！
我们的agent认为1号机臂对于3 号赌博机是最优决策
...经检验正确！

希望这篇文章可以帮助你直观地理解强化学习中agent如何处理复杂的交互问题。掌握本文中的内容之后，你可以在下一篇文章中进一步探索时间和行为共同作用的问题。

系列文章（翻译进度）：

1. (0) Q-Learning的查找表实现和神经网络实现
2. (1) 双臂赌博机
3. (1.5) — 上下文赌博机
4. Part 2 — Policy-Based Agents
5. Part 3 — Model-Based RL
6. Part 4 — Deep Q-Networks and Beyond
7. Part 5 — Visualizing an Agent’s Thoughts and Actions
8. Part 6 — Partial Observability and Deep Recurrent Q-Networks
9. Part 7 — Action-Selection Strategies for Exploration
10. Part 8 — Asynchronous Actor-Critic Agents (A3C)